第31章 海量数据处理的数据结构和算法《下》

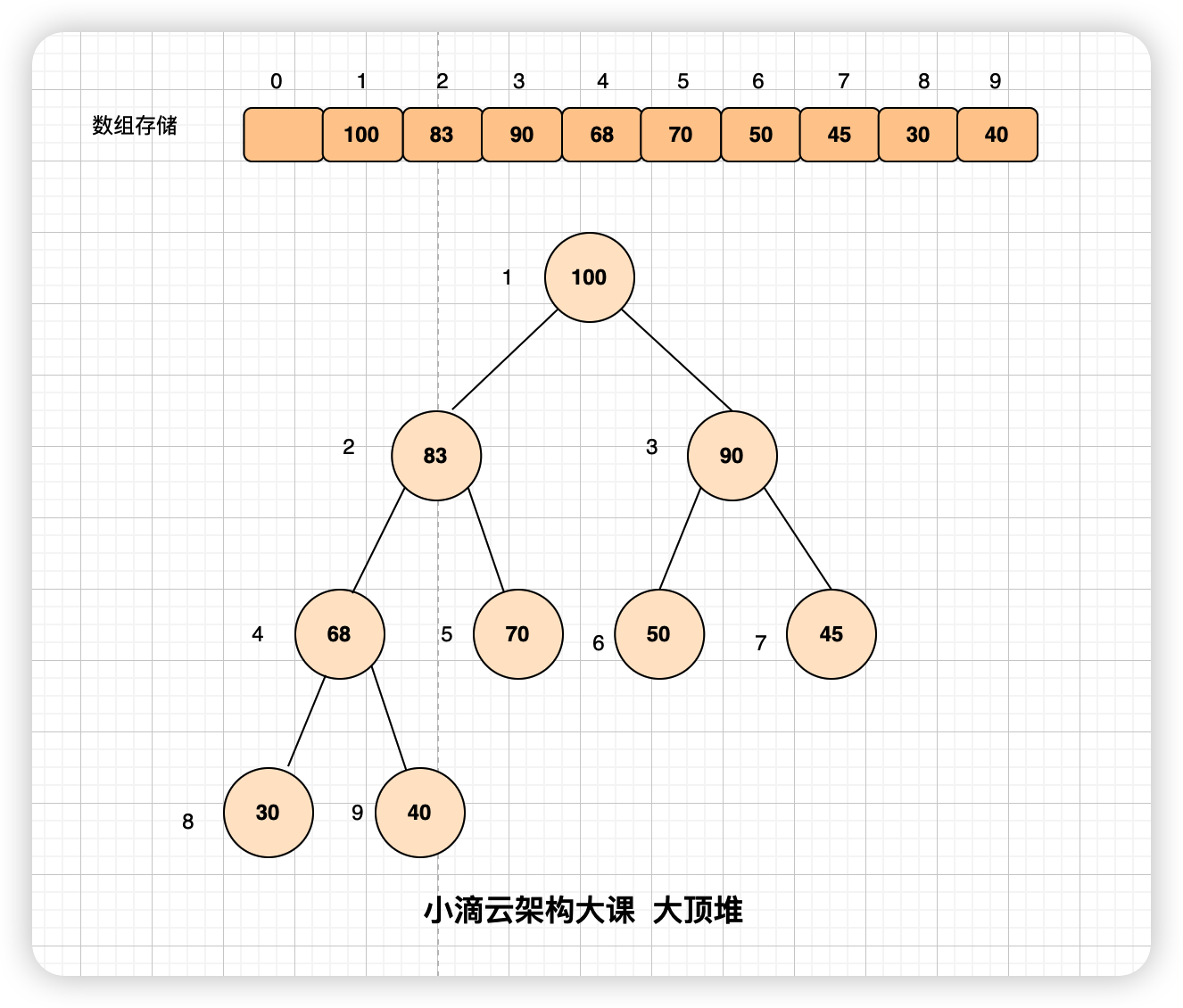
第 1 集 核心排序算法之堆排序原理讲解

简介： 重点排序算法之堆排序原理讲解

• 什么是堆排序

  • 指利用堆这种数据结构所设计的一种排序算法，将二叉堆的数据进行排序，构建一个有序的序列

  • 排序过程中，只需要个【别临时存储】空间，所以堆排序是原地排序算法，空间复杂度为 O(1)

    • 本身大顶堆和小顶堆里面的元素是无序的，只是有一定的规则在里面
    • 大顶堆，每个父节点的值都大于或等于其子节点的值，即根节点的值最大
    • 小顶堆，每个父节点的值都小于或等于其子节点的值，即根节点的值最小
    

  • 过程分为建堆和排序两大步骤

    • 【建堆】过程的时间复杂度为 O(n)，排序过程的时间复杂度为 O(nlogn)，所以 堆排序整体的时间复杂度为 O(nlogn）

    • 【堆排序】不是稳定的算法，在排序的过程中，将堆最后一个节点跟堆顶节点互换，可能改变值相同数据的原始相对顺序，

  • 流程

    • 把无序数组构建成二叉堆，建堆结束后，整个序列的最大值就是堆顶的根节点
    • 将其与末尾元素进行交换(删除操作), 堆顶 a[1]与最后一个元素 a[n]交换，最大元素放到下标为 n 的位置, 末尾就为最大值
    • 然后将剩余 n-1 个元素重新构造成一个堆（堆化操作），这样会得到 n 个元素的次小值
    • 反复执行上述步骤，得到一个有序的数组

• 堆排序动画演示

  • 站点：https://www.cs.usfca.edu/~galles/visualization/HeapSort.html

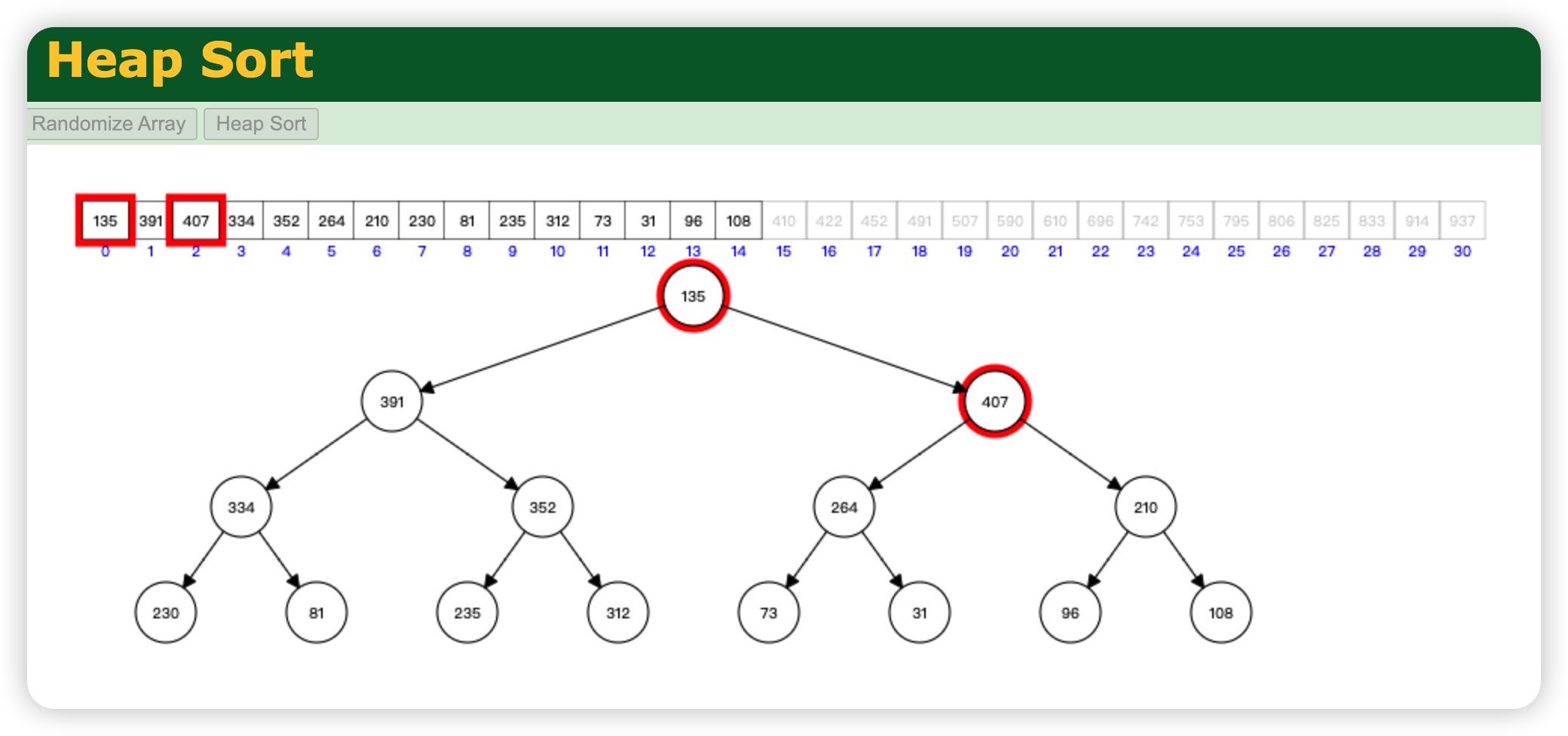
第 2 集 核心排序算法之堆排序编码实战《上》

简介： 核心排序算法之堆排序编码实战《上》

• 编码实现
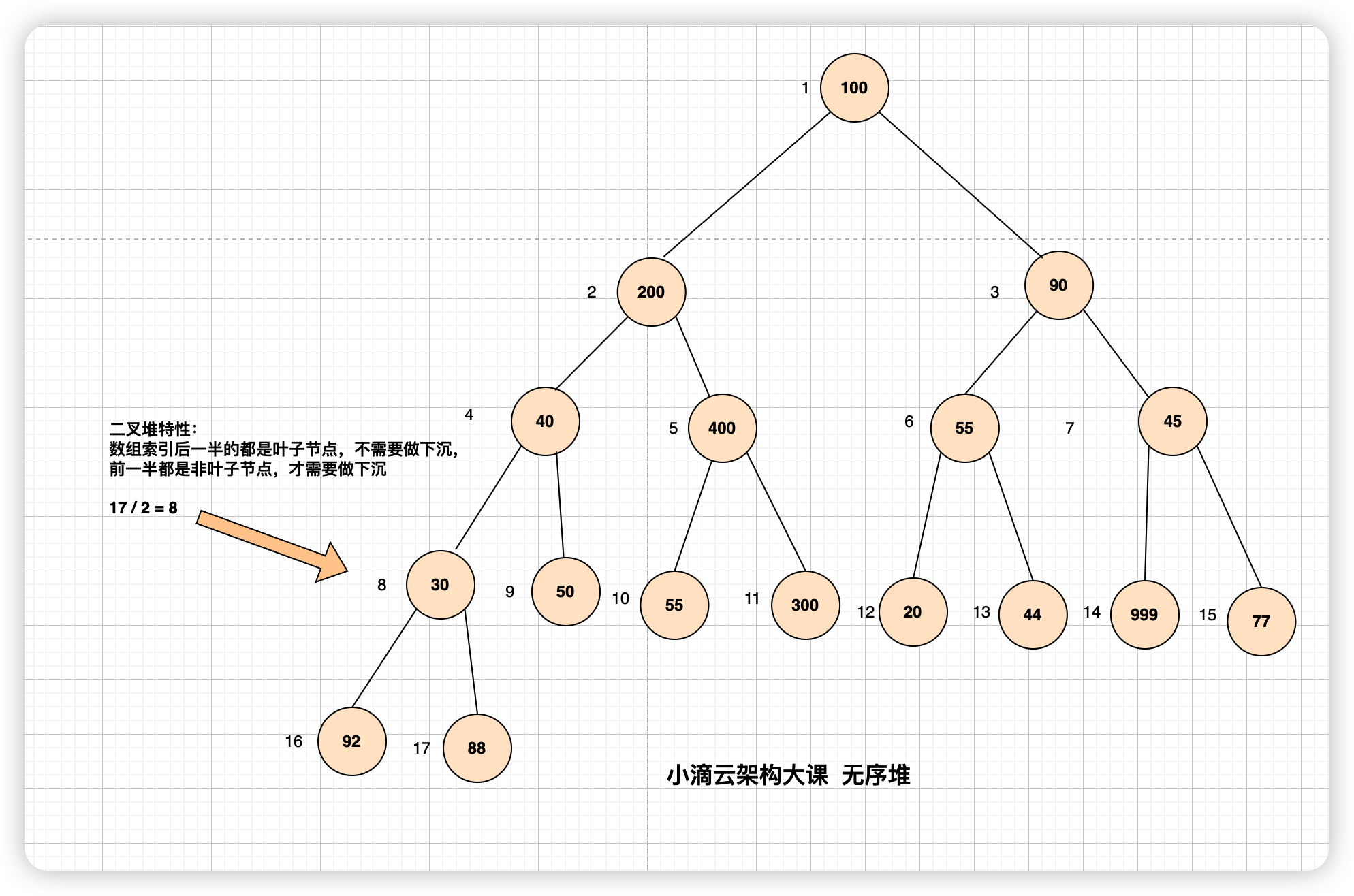
  • 无序堆构建成二叉堆
  • 利用二叉堆特性：数组索引一半后的都是叶子节点，不需要做下沉比较；一半前都是非叶子节点，才需要做下沉比较

public class HeapSort {

    /**
     * 从小到大进行堆排序
     * @param source
     */
    public static void sort(int[] source) {
        //步骤一：构建堆，数组下标0不存储数据
        int[] heap = new int[source.length + 1];

        //根据待排序数组，构造一个无序的堆
        System.arraycopy(source, 0, heap, 1, source.length);

        //对堆中的元素做下沉调整，从长度的一半处开始，往堆顶索引1处扫描)
        //二叉堆特性：数组索引一半后的都是叶子节点，不需要做下沉，一半前都是非叶子节点，才需要做
        for (int i = (heap.length) / 2; i > 0; i--) {
            down(heap, i, heap.length - 1);
        }
        System.out.println("大顶堆："+Arrays.toString(heap));


        // 步骤二：堆排序
    }


    /**
     * 比较大小,item[left] 元素是否小于 item[right]的元素
     */
    private static boolean rightBig(int[] heap, int left, int right) {
        return heap[left] < heap[right];
    }

    /**
     * 交互堆中两个元素的位置
     */
    private static void swap(int[] heap, int i, int j) {
        int temp = heap[i];
        heap[i] = heap[j];
        heap[j] = temp;
    }


    /**
     * 使用下沉操作，堆顶和最后一个元素交换后，重新堆化
     * 不断比较 节点 arr[k]和对应 左节点arr[2*k] 和 右节点arr[2*k+1]的大小，如果当前结点小，则需要交换位置
     * 直到找到 最后一个索引节点比较完成  则结束
     * <p>
     * 数组中下标为 k 的节点
     * 左子节点下标为 2*k 的节点
     * 右子节点就是下标 为 2*k+1 的节点
     * 父节点就是下标为 k/2 取整的节点
     */
    private static void down(int[] heap, int k, int range) {
        // 最后一个节点的下标是range，即元素总个数
        while (2 * k <= range) {

            //记录当前节点的左右子节点，较大的节点
            int maxIndex;

            if (2 * k + 1 <= range) {
                if (rightBig(heap, 2 * k, 2 * k + 1)) {
                    maxIndex = 2 * k + 1;
                } else {
                    maxIndex = 2 * k;
                }
            } else {
                maxIndex = 2 * k;
            }

            //比较当前节点和较大接的值，如果当前节点大则结束
            if (heap[k] > heap[maxIndex]) {
                break;
            } else {
                //否则往下一层比较，当前节点的k变为子节点中较大的值
                swap(heap, k, maxIndex);
                k = maxIndex;
            }

        }
    }

}

第 3 集 核心排序算法之堆排序编码实战《下》

简介： 核心排序算法之堆排序编码实战《下》

• 编码实现

    /**
     * 从小到大进行堆排序
     * @param source
     */
    public static void sort(int[] source) {
        //步骤一：构建堆，数组下标0不存储数据
        int[] heap = new int[source.length + 1];

        //根据待排序数组，构造一个无序的堆
        System.arraycopy(source, 0, heap, 1, source.length);

        //对堆中的元素做下沉调整，从长度的一半处开始，往堆顶索引1处扫描)
        //二叉堆特性：数组索引一半后的都是叶子节点，不需要做下沉，一半前都是非叶子节点，才需要做
        for (int i = (heap.length) / 2; i > 0; i--) {
            down(heap, i, heap.length - 1);
        }
        System.out.println("大顶堆："+Arrays.toString(heap));


        // 步骤二：堆排序，把堆顶元素和数组最后一个索引元素交换；然后再堆化，然后堆顶又是最大元素，再和数组倒数第二索引处交换；持续进行直到最后
        // 类似删除操作，只需要下沉操作重新堆化即可

        //记录未排序的元素中最大的索引
        int maxUnSortIndex = heap.length - 1;
        //通过循环，交换堆顶元素和最大未排序元素的下标
        while (maxUnSortIndex != 1) {
            //交换元素
            swap(heap, 1, maxUnSortIndex);
            //排序后最大元素所在的索引，不要参与堆的下沉，所以 递减1
            maxUnSortIndex--;

            //继续对堆顶处的元素进行下沉调整
            down(heap, 1, maxUnSortIndex);
        }

        //把heap中的数据复制到原数组source中
        System.arraycopy(heap, 1, source, 0, source.length);

    }

• 测试

 public static void main(String[] args) {
        //待排序数组
        int[] arr = {923,23,12,4,9932,11,34,49,123,222,880};
        //堆排序
        HeapSort.sort(arr);
        //输出排序后数组中的元素
        System.out.println("堆排序:"+Arrays.toString(arr));
}

第 4 集 大厂超高频面试题-海量数据之堆应用 TopK 思想

简介：大厂超高频面试题-海量数据之堆应用 TopK 思想

• TopK 问题

  • 从一堆数据中选出前多少个最大或最小数，这类是一二线大厂特别高频的面试题
  • 思想
    • 用堆来解决问题，【取大用小，取小用大】
    • 取最大的 K 个数 用小顶堆；
    • 取最小的 K 个数 用大顶堆；

• 取海量数据里面最小的 K 个数

  • 要找出数组中最小的 k 个数，就要【构造一个有 k 个元素的大顶堆】，大顶堆的堆顶元素值最大
  • 比较堆顶的元素和扫描的元素，如果堆顶元素 < 扫描元素，继续扫描其他元素
  • 如果堆顶元素 > 扫描元素 ，将堆顶元素出队，扫描元素插入大顶堆，将更小的元素换到堆中
  • 反复根据上述步骤操作，直到比较完最后一个元素，此时堆里面的就是最小的 k 个数

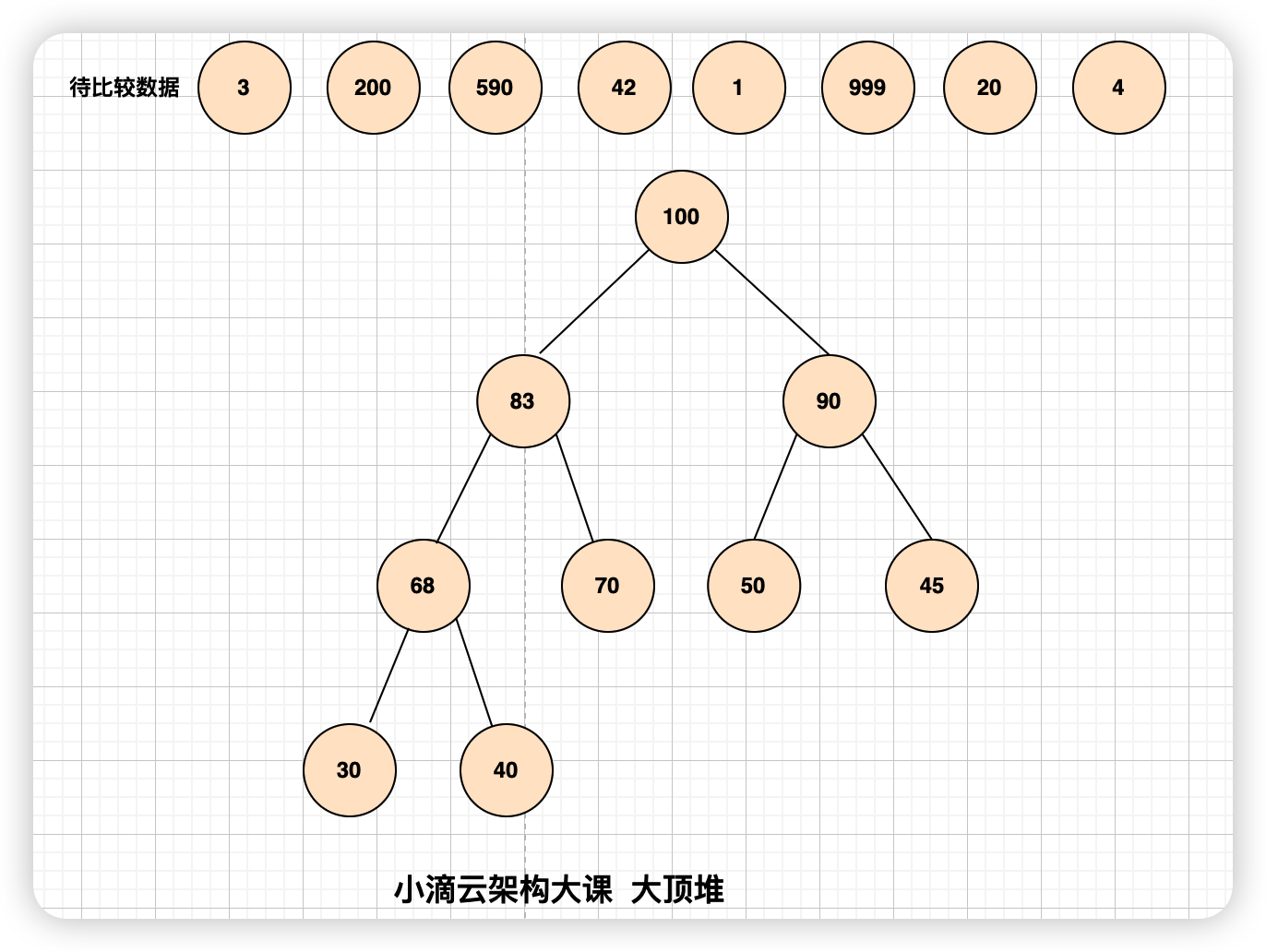
• 取海量数据里面最大的 K 个数
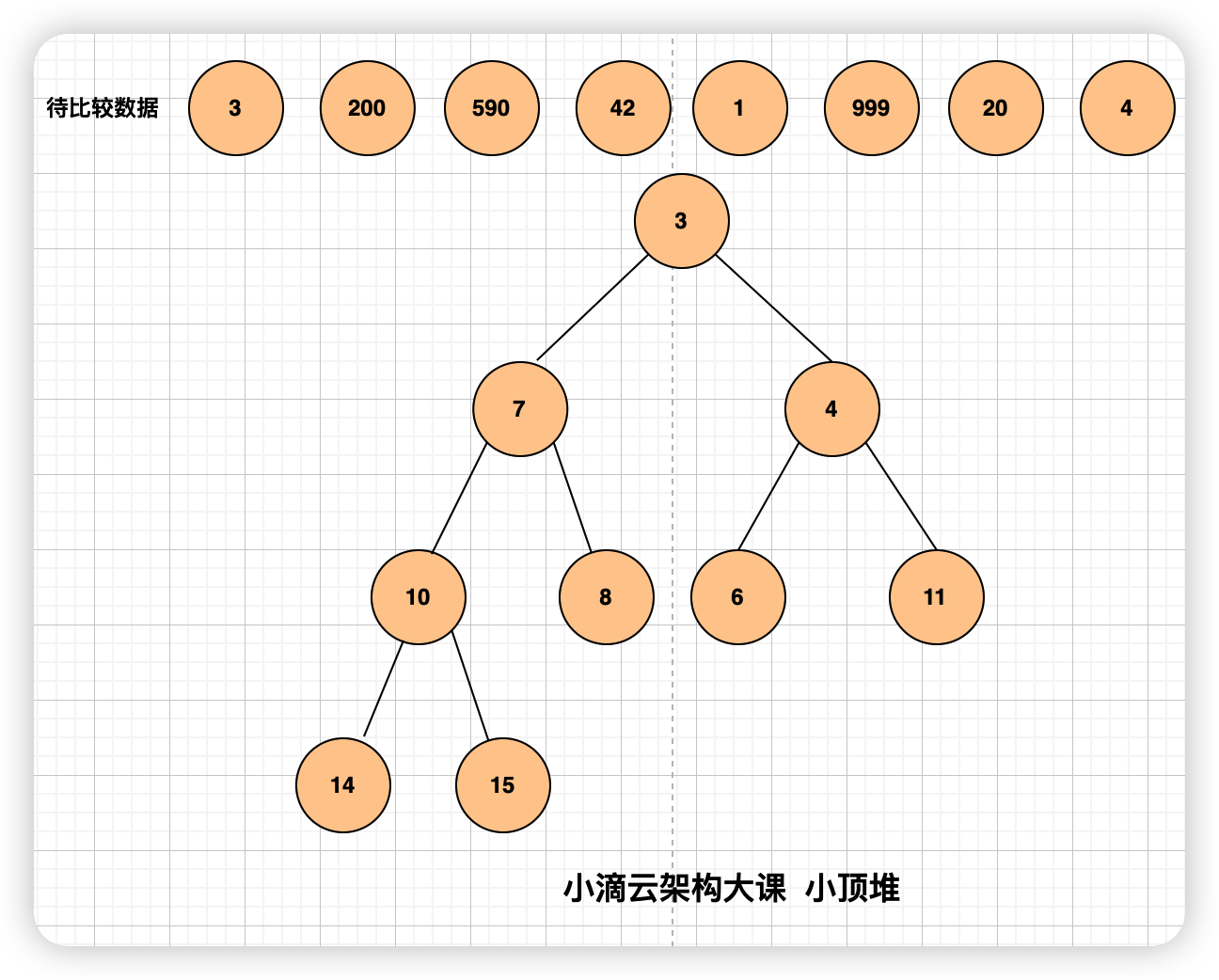
  • 要找出数组中最大的 k 个数，就要【构造一个有 k 个元素的小顶堆】，小顶堆的堆顶元素值最小
  • 比较堆顶的元素和扫描的元素，如果堆顶元素 > 扫描元素，继续扫描其他元素
  • 如果堆顶元素 < 扫描元素 ，将堆顶元素出队，扫描元素插入小顶堆，将更大的元素换到堆中
  • 反复根据上述步骤操作，直到比较完最后一个元素，此时堆里面的就是最大的 k 个数

第 5 集 大厂超面试题-100 亿个数中找出最小的前 k 个数《上》

简介：大厂超面试题-100 亿个数中找出最小的前 k 个数《上》

• 需求

  • 100 亿个数中找出最小的前 k 个数

• 题目分析

  • 100 亿个数，一个数占四个字节，那么 100 亿个数就需要 40G 的存储空间

    • 1G = 10 亿字节, 100 亿个 int = 400 亿字节 = 40G

  • 使用普通的电脑和服务器肯定不可能把全部数据，不能创建一个具有 100 亿个数据的堆

  • 而且使用常规加载进去，存储空间不够大，时间复杂度也是很大

• 解题思路

  • 要找出数组中最小的 k 个数，就要【构造一个有 k 个元素的大顶堆】，大顶堆的堆顶元素值最大
  • 比较堆顶的元素和扫描的元素，如果堆顶元素 < 扫描元素，继续扫描其他元素
  • 如果堆顶元素 > 扫描元素 ，将堆顶元素出队，扫描元素插入大顶堆，将更小的元素换到堆中
  • 反复根据上述步骤操作，直到比较完最后一个元素，此时堆里面的就是最小的 k 个数

• 代码

public class MinTopKHeapSort {

    /**
     * 从小到大进行堆排序
     * @param source
     */
    public static void sort(int[] source,int temp) {
        //步骤一：构建堆，数组下标0不存储数据
        int[] heap = new int[source.length + 1];

        //根据待排序数组，构造一个无序的堆
        System.arraycopy(source, 0, heap, 1, source.length);

        //对堆中的元素做下沉调整，从长度的一半处开始，往堆顶索引1处扫描)
        //二叉堆特性：数组索引一半后的都是叶子节点，不需要做下沉，一半前都是非叶子节点，才需要做
        for (int i = (heap.length) / 2; i > 0; i--) {
            down(heap, i, heap.length - 1);
        }
        System.out.println("大顶堆："+Arrays.toString(heap)+", 新元素="+temp);


        // 循环将数组中剩余的数放入heap数组中，并进行堆排序，如果当前数小于Heap数组中的第一个数,则将当前数替换为第一个数
        if (temp < heap[1]) {
            heap[1] = temp;
            //重新堆化
            down(heap, 1, source.length-1);
        }
        System.arraycopy(heap, 1, source, 0, source.length);

    }

    /**
     * 比较大小,item[left] 元素是否小于 item[right]的元素
     */
    private static boolean rightBig(int[] heap, int left, int right) {
        return heap[left] < heap[right];
    }

    /**
     * 交互堆中两个元素的位置
     */
    private static void swap(int[] heap, int i, int j) {
        int temp = heap[i];
        heap[i] = heap[j];
        heap[j] = temp;
    }


    /**
     * 使用下沉操作，堆顶和最后一个元素交换后，重新堆化
     * 不断比较 节点 arr[k]和对应 左节点arr[2*k] 和 右节点arr[2*k+1]的大小，如果当前结点小，则需要交换位置
     * 直到找到 最后一个索引节点比较完成  则结束
     */
    private static void down(int[] heap, int k, int range) {


    }

    public static void main(String[] args) {
        //随机数据
        int[] arr = {923,982,23,1000,1990,12,4,9932,11,34,49,123,1,222,880};

        // 定义一个长度为k的数组
        int top = 3;
        int[] heap = new int[top];

        // 循环将数组中的前k个数放入Heap数组中；
        for (int i = 0; i < top; i++) {
            heap[i] = arr[i];
        }

        //循环将数组中剩余的数放入heap数组中，并进行堆排序
        for(int i = top; i < arr.length; i++){
            MinTopKHeapSort.sort(heap,arr[i]);
        }

        //输出排序后数组中的元素
        System.out.println("最小的 top k 数据:"+Arrays.toString(heap));

    }

}

第 6 集 大厂超面试题-100 亿个数中找出最小的前 k 个数《下》

简介：大厂超面试题-100 亿个数中找出最小的前 k 个数《下》

• 下沉操作方法另外一种

    /**
     * 简单写法
     */
    private static void siftDown(int[] arr, int i, int length) {
        //当前节点存在左子树
        while (2 * i < length) {
            //此时j为左子树节点
            int j = 2 * i;
            //如果当前节点存在右子树，并且右子树的值大于左子树的值
            if (j < length && arr[j + 1] > arr[j]) {
                //此时j为右子树节点
                j = j + 1;
            }
            //比较当前节点值与其左右子树值的大小
            if (arr[i] > arr[j]) {
                break;
            } else {
                swap(arr, i, j);
                i = j;
            }
        }
    }

• 测试

• 延伸

  • 题目除了堆排序，也有其他解法

  • 如果是百亿数据，只需要从文本中读取前 k 个出来,然后构建大顶堆，然后在从剩余的元素逐个读取比较即可