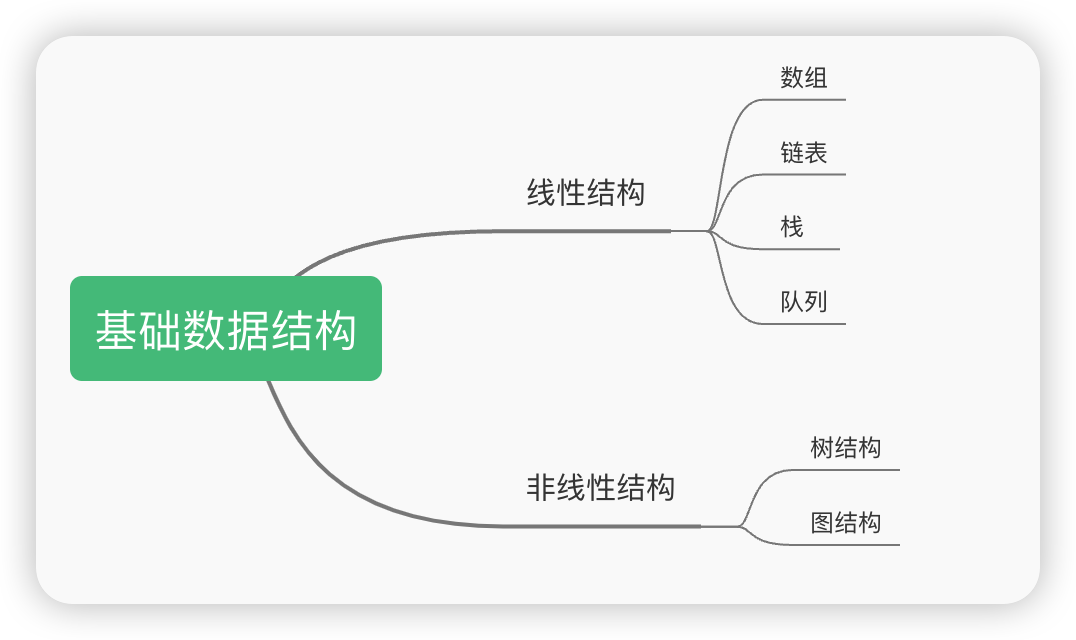
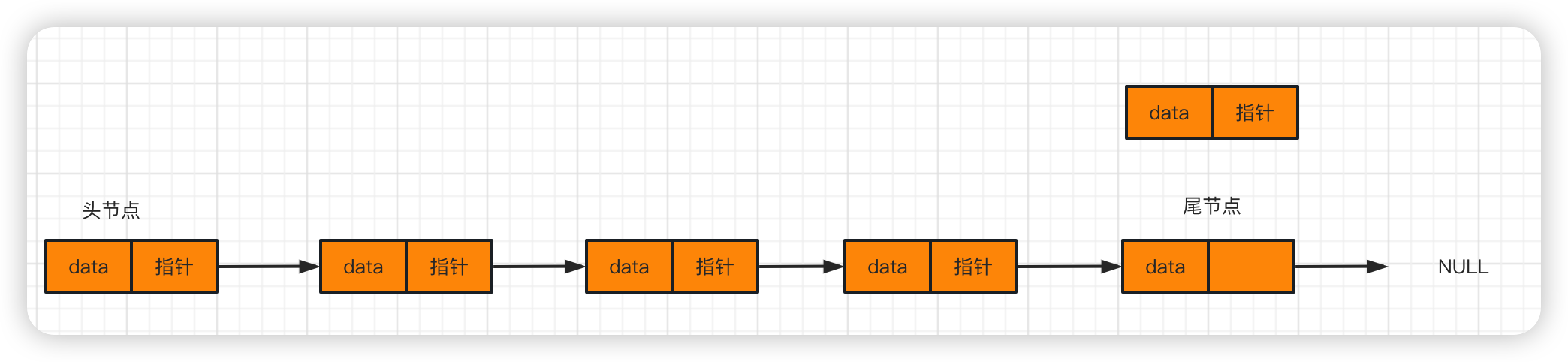
第26章 大厂业务高频的数据结构和算法介绍

2025/04/11
posted in
数据结构和算法