第29章 架构师必备的二叉树演进和底层原理

第 1 集 二叉树演进之 BST 二叉查找树底层原理和缺点

简介： 二叉树演进之 BST 二叉查找树底层原理和缺点

• 注意
  • 树相关算法会比较多，且相对复杂点，重点掌握原理
  • 课程会用动图与文字结合的形式，更容易的理解算法的本质

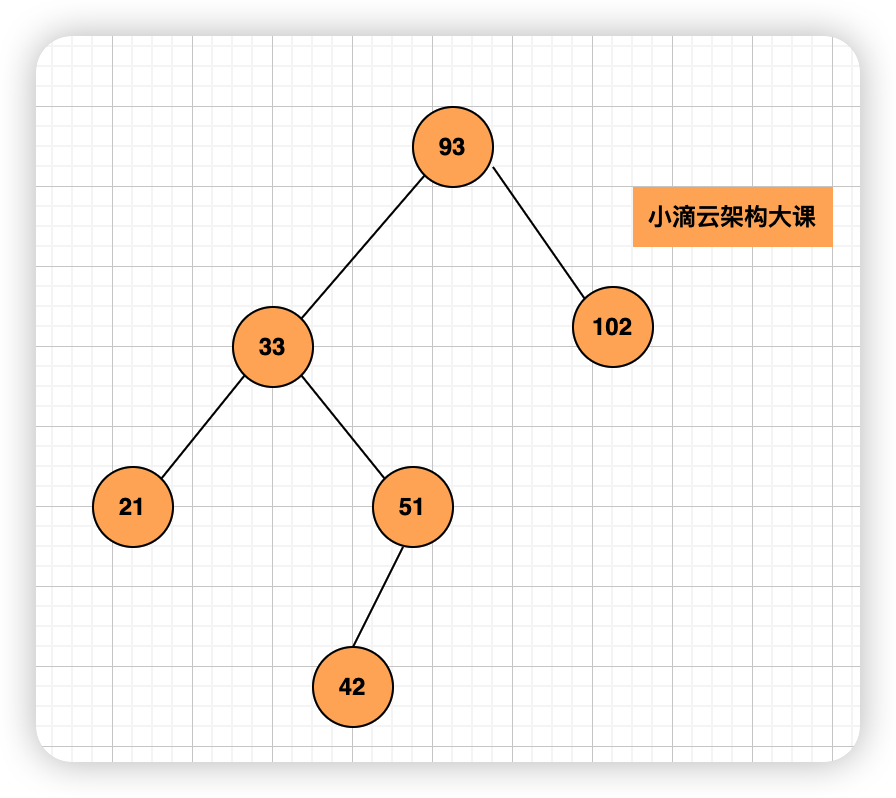
• 二叉查找树（二叉排序树）

  • Binary Search Tree，简称 BST，二叉树中最常用的一种类型，也叫二叉排序树
  • 特征
    • 在树中任意一个节点，左子树中的每个节点的值，都要小于这个节点的值，右子树的值都大于这个节点的值
    • 二叉查找树的查找、插入和删除操作的平均时间复杂度都是 O(logn)，n 为树中的节点数，是一种非常有效的查找数据结构。
    • 依赖于它特殊的结构，可以支持快速的查找，插入，删除一个数据

• 线性表查找和二叉查找树效率对比

  • 动画效果演示

    • 网站：https://www.cs.usfca.edu/~galles/visualization/Algorithms.html

• 问题点

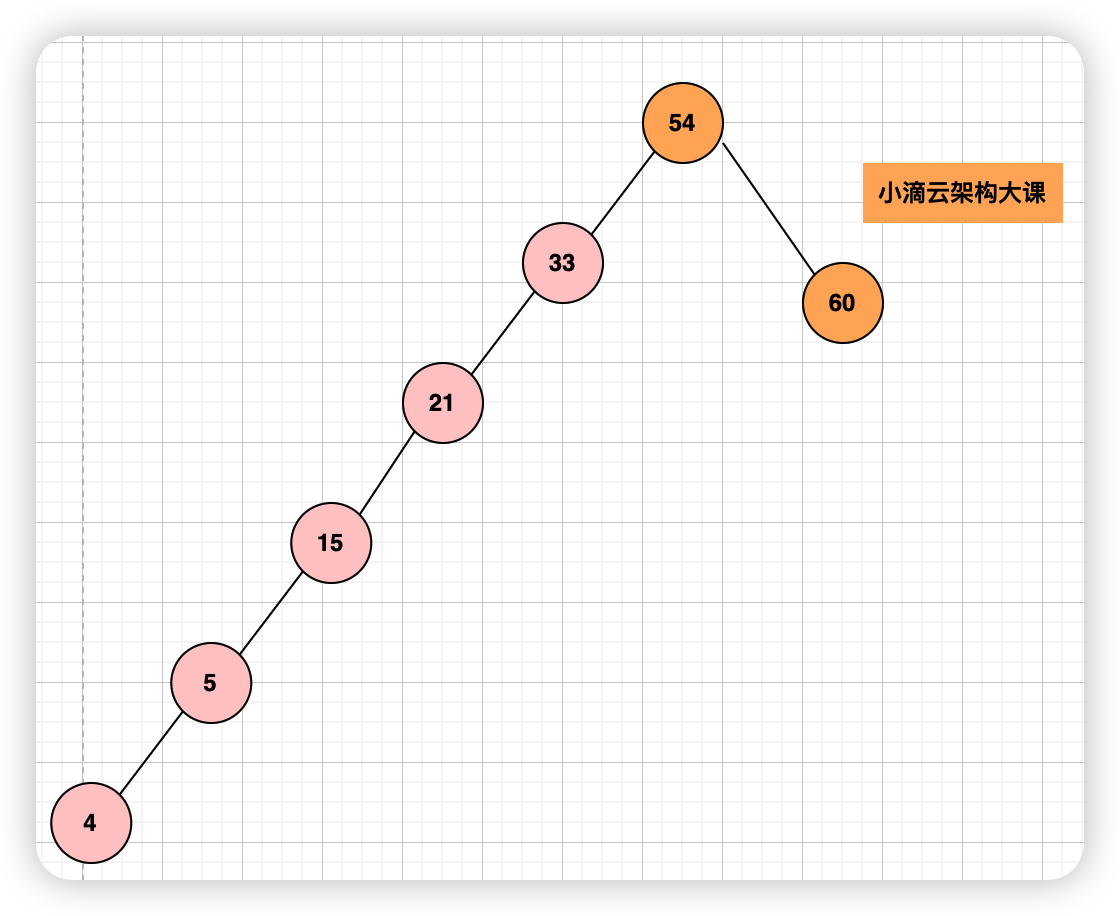
  • 在数据糟糕的情况下，二叉查找树左右子树极度不平衡，退化成为链表时候，相当于全表扫描，时间复杂度就变为了 O(n)
  • 最好情况下，当二叉查找树是一棵完全二叉树或者满二叉树时，时间复杂度和树的高度成正比，也就是 O(高度)。
  • 完全二叉树的高度小于等于 log2n（n 为节点个数），在最好情况下，二叉查找树的时间复杂度为 O(logn)
  • 那咋办？

第 2 集 二叉树演进之 AVL 平衡二叉树底层原理

简介： 二叉树演进之 AVL 平衡二叉树底层原理

• 背景
  • 二叉查找树左右子树极度不平衡，退化成为链表时候，相当于全表扫描，时间复杂度就变为了 O(n)
  • 插入速度没影响，但是查询速度变慢，比单链表都慢，每次都要判断左右子树是否为空
  • 需要保证二叉查找树一直保持平衡，就需要用到平衡二叉树

• 平衡二叉树（Balanced Binary Tree）

  • 称为 AVL 树（Adelson-Velskii 和 Landis）平衡二叉查找树 是一种特殊的二叉查找树每个节点的左右子树的高度差不能超过 1
  • 平衡二叉树保证了树的构造是平衡的，当插入或删除数据导致不满足平衡二叉树不平衡时，会进行调整树上的节点来保持平衡
  • 平衡二叉树的插入和删除操作都是 O(logn)的，因此它的查找性能很高，比非平衡的二叉查找树要快得多
  • 实现方式：红黑树、 Treap、伸展树等

• 练习：下面哪个是平衡二叉树

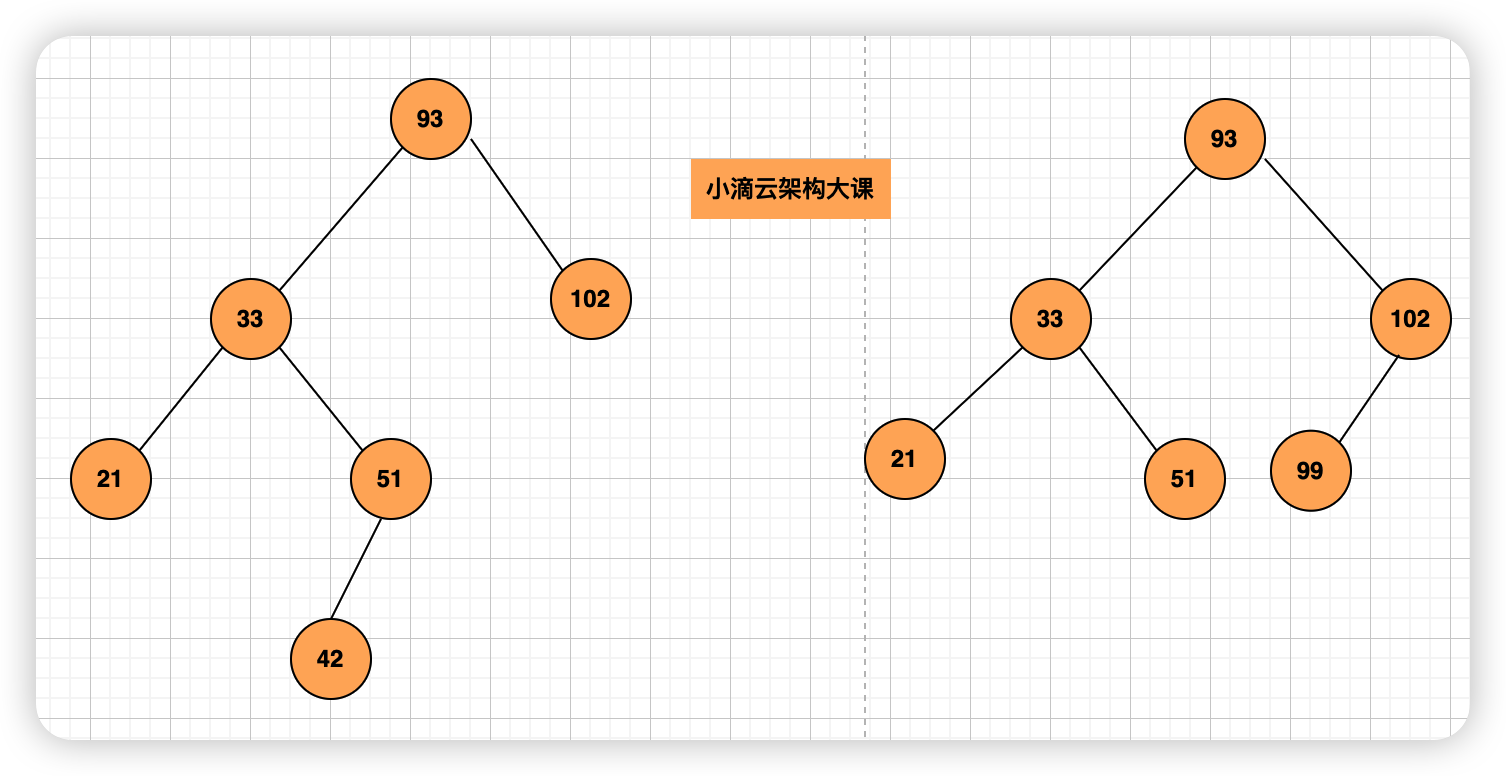
• 核心思想

  • 在插入或删除节点时，如果发现子树不平衡，则对子树进行旋转操作，使其重新达到平衡

  • 旋转操作有三种，哪边高度底就哪边旋转， 提升高度

    • 左旋 LL 旋转
    • 右旋 RR 旋转
    • 左右 LR 双旋 和 右左 RL 双旋

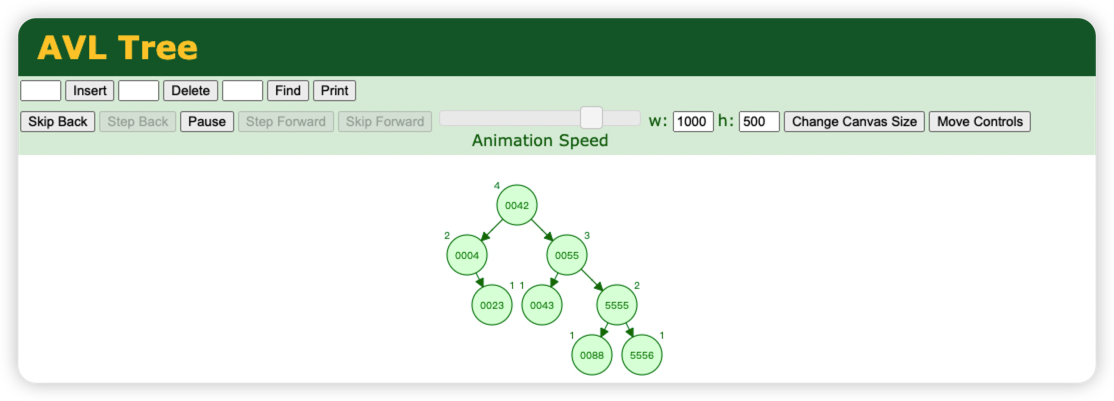
• 动画效果演示

  • 网站：https://www.cs.usfca.edu/~galles/visualization/AVLtree.html

  

• 问题点

  • 查找操作
    • 二叉搜索树的时间复杂度介于 O(log2N)到 O(n)之间
    • 如果退化成单链表，时间复杂度就是顺序查找，为 O(n)
    • 如果是平衡二叉树，查找效率会提高到 O(log2N)
  • 例子
    • 平衡二叉树的高度就等于每次查询数据时磁盘 IO 操作的次数。
    • 假如磁盘每次寻道时间为 10ms，在表数据量大时，查询性能就会很差
    • 1 百万的数据量，log2(N)约等于 20 次磁盘 IO，时间 20*10=0.2s
      • log2(N) 相当于 2 的多少次方（立方）等于 N，例：log2 (8）= 3
      • 2 的 20 次方=1048576，所以就是 20 次磁盘 IO
  • 不支持范围查询快速查找，范围查询时需要从根节点多次遍历，查询效率比较低

第 3 集 二叉树的演进之多叉树和 B-Tree 树原理

简介： 二叉树的演进之多叉树 B-Tree 树和应用

• 背景

  • 平衡二叉树操作效率高，但是存在不少问题，常规需要把树加载到内存里面
  • 如果节点少则没问题，但是如果节点多 则高度很大，进行 IO 操作则存在性能问题
  • 场景
    • 平衡二叉树每个节点只存储一个键值和数据的，每个磁盘块仅仅存储一个键值和数据
    • 如果要存储海量的数据，那构建平衡二叉树的时候耗时多
    • 如果平衡二叉树的节点将会非常多，高度也会极其高，查找数据时会进行很多次磁盘 IO，效率将会极低
  • 为了解决平衡二叉树的这个问题，设计一种单个节点可以存储多个键值和数据的平衡树，也就是我们接下来要说的 多叉树

• 多叉树

  • 也叫 多路查找树（muitl-way search tree）
  • 每一个节点的子树可以多于两个，且每一个节点处可以存储多个元素，常见的就是 B 树、B+树等
    • 注意：B 是 Balanced 意思，不是 Binary 的意思
  • 多叉树通过重新组织节点，降低了树的高度，可以提高 IO 效率
  
  • 应用
    • 操作系统 IO 操作都会利用磁盘预读原理，如果一个节点大小是一个存储页（4KB）
    • 存储每个节点只需要一次 IO 即可完成存储
    • B 树在存储系统里面广泛应用，比如数据库系统、文件系统等

• 多叉查找树之 B 树

  • 特点

    • 也叫 B-Tree，B-树，全称是 Balanced Tree，是一种多路平衡查找树
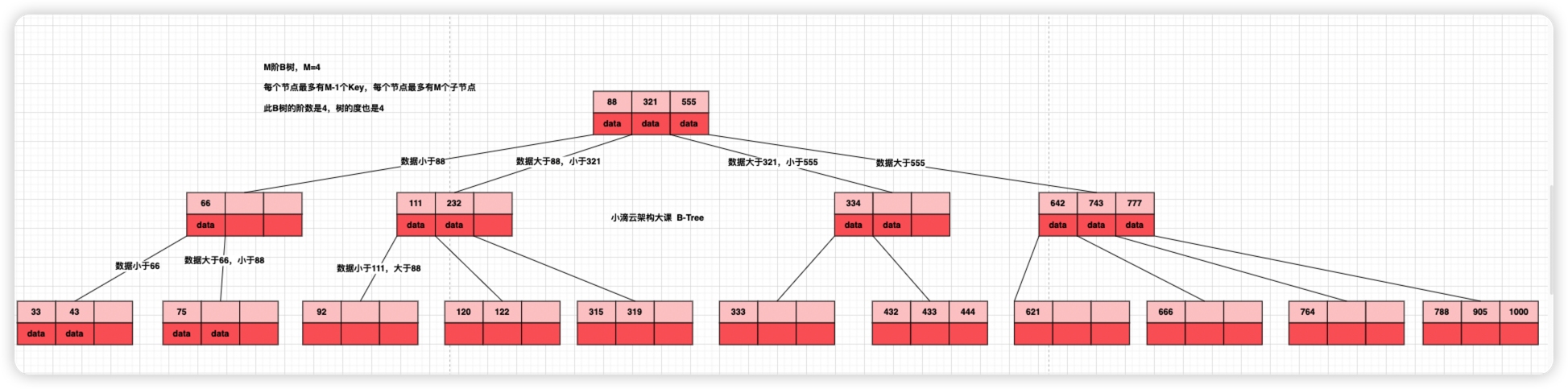
    • 一个节点包括多个 key (数量看业务)，具有 M 阶的 B 树，每个节点最多有 M-1 个 Key
    • 节点的 key 元素个数就是指这个节点能够存储几个数据
    • 每个节点最多有 m 个子节点，最少有 M/2 个子节点，其中 M>2
    • 数据集合分布在整个树里面，叶子节点和非叶子节点都存储数据；类似在整个树里面做一次二分查找
    • B 树相对于平衡二叉树，每个节点存储了更多的键值（key）和数据（data）
    • 实际业务中 B 树的阶数一般大于 100，存储大量数据，B 树高度也会很低，查询效率会更高,
    • 备注
      • 每个节点拥有最多的子节点，子节点的个数一般称为阶；
      • 阶：m 阶是代表每个节点最多有 m 个分支（子树）
      • 树的度：这棵树里面节点最大的度
      • 节点的度：当前节点有几个孩子

  • B 树图案例

  

  • 动画效果演示
    • 网站：https://www.cs.usfca.edu/~galles/visualization/BTree.html

第 4 集 B 树插入流程讲解和在文件系统里磁盘 IO 应用

简介： B 树插入流程讲解和在文件系统的磁盘 IO 应用

• B 树插入原理

  • 每个节点的数据都是顺序存储，具有 M 阶的 B 树，树的阶数表示每个结点最多可以有多少个子结点
  • 插入流程讲解
    • 网站：https://www.cs.usfca.edu/~galles/visualization/BTree.html

• B 树的应用场景

  • 在数据库中，B 树用来维护索引，用来提高查询效率，一个节点可以存储整个页（即磁盘块）
  • 在文件系统中，B 树用来存储文件的目录信息，提高文件的访问效率
  • 在操作系统中，B 树可以用来存储内存管理信息，提高内存的分配效率

• 磁盘 IO 为例子

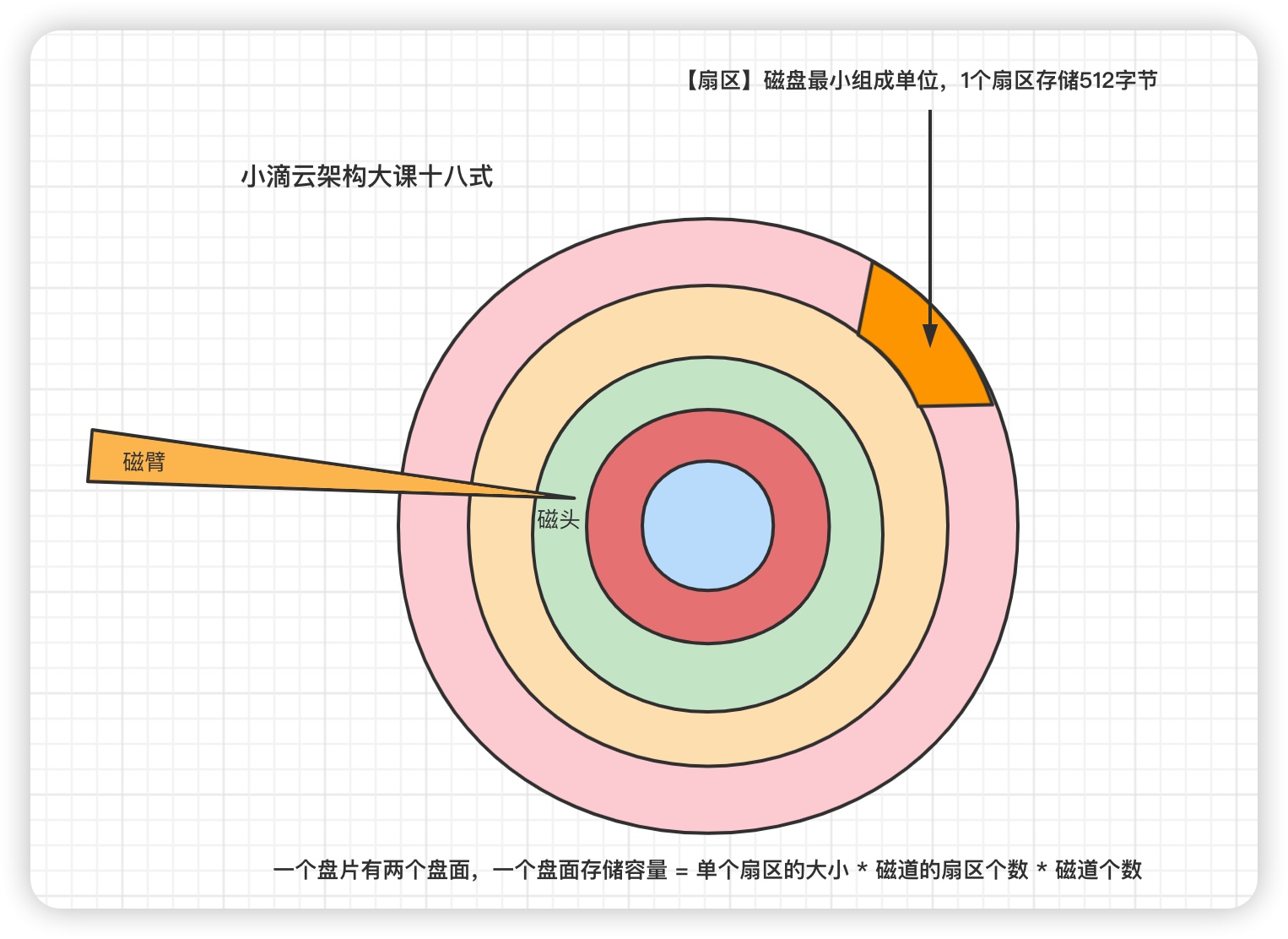
  • 回顾基础：

    • 从磁盘读取数据耗时 为：寻道时间+旋转时间+读取时间

    • 如何读取数据：

      • 磁臂摆动+盘片转动（耗时大所以导致慢，随机在硬盘上找一个数据，需要 8-14 ms），定位到目标扇区读取数据

      • 磁臂在一定范围内摆动，来找到目标扇区，靠磁头把某个扇区的数据传输到总线上

      • 磁臂摆动范围有限，触达不到比较远的扇区，靠转轴来带动盘片，比如磁盘转速有 7200 转/分，1 秒就是 120 圈

      • 常规 1 秒可以做 100 次随机 IO，所以高并发业务单靠磁盘上扛不住的，基本都是要结合缓存

    • 概念划分

      • 磁盘读写的最小单位是扇区 sector，常规扇区是 512Byte，这样的话读写单位太小，性能不高
    • 文件系统把连续的扇区组成逻辑块 block，以逻辑块为最小单元来管理数据
      • 一般逻辑块大小为 4KB（也称为 页），是由连续的 8 个扇区组成

    

  • 磁盘为了提高读取效率，根据局部性原理，有预读的特性，即磁盘不是严格按需读取，每次都会预读部分数据放到内存中

  • 页是计算机存储逻辑块，一般是是 1024 字节或者整数倍，预读的数一般是页大小或者整数倍

  • 操作系统 IO 操作都会利用磁盘预读原理，如果一个节点大小是一个存储页（假如 4KB），每个节点只需要一次 IO 即可完成存储

  • 面试题：3 层的 B 树，阶数为 1024，最多容纳多少个元素

    • B 树的阶数表示每个结点最多可以有多少个子结点，因此 B 树的阶数为 1024，表示每个结点最多可以有 1024 个子结点

    • 由于 B 树的 3 层，因此根结点可以有 1024 个子结点，每个子结点又可以有 1024 个子结点

    • 因此一个 3 层的 B 树，阶数为 1024，B 树的每一层的节点数都是阶数的幂次方

    • 计算总容量 把每一层的节点数相加 即 1024^1+1024^2+1024^3 大约是 11 亿个节点，假如每个节点放一个元素就是 11 亿个

    • 所以在 10 亿个数据中找目标值，常规小于 3 次磁盘 IO 即可找到目标值，比平衡二叉树的 30 次提升了不少

      • 平衡二叉树的高度就等于每次查询数据时磁盘 IO 操作的次数。

      • 10 亿的数据量，log2(N)约等于 30 次磁盘 IO，

        • log2(N) 相当于 2 的多少次方（立方）等于 N，例：log2 (8）= 3
        • 2 的 30 次方=1073741824，所以就是 30 次磁盘 IO

第 5 集 核心数据结构之 B+Tree 树底层原理讲解

简介： 核心数据结构之 B+Tree 树底层原理讲解

• B+Tree （B-Tree）

  • 是 B 树的一种变形形式，B+树上的叶子结点存储关键字以及相应记录的地址，同等存储空间下比 B-Tree 存储更多 key
  • 非叶子节点不对关键字记录的指针进行保存，只进行数据索引 , 树的层级会更少 , 所有叶子节点都在同一层,
  • 叶子节点的关键字从小到大有序排列，叶子节点之间用指针连接, 构成有序链表（稠密索引）
  • B+树上每个非叶子节点之间是一个双向链表进行链接，而叶子节点中的数据都是使用单向链表链接
  • 查找特点
    • 当索引部分某个结点的关键字与所查的关键字相等时，并不停止查找
    • 继续沿着关键字的指针向下，每次查询必须到叶子节点才能真正获取到相关数据
    • B+Tree 叶子节点相连接，对树的遍历就是只需要 一次线性遍历叶子节点
    • 由于叶子节点的数据是顺序排列，方便区间查找
    • 在 B+树完成范围查找，排序查找，分组查找，去重查找 比 B 树效率也比较高
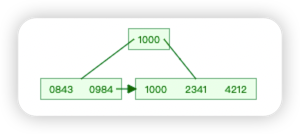
  • 示例图讲解

• B+Tree 插入流程解析

  • 动画地址 https://www.cs.usfca.edu/~galles/visualization/BPlusTree.html

• 总结

  • B 树和 B+树的最大区别在于非叶子节点是否存储数据
  • B+树非叶子节点只是当索引使用，同等空间下 B+树存储更多 key
  • B 树,非叶子节点和叶子节点都会存储数据，找到对应节点就有对应的数据
  • B+树, 只有叶子节点才会存储数据,存储的数据都是在一行上，找到非叶子节点的 key，还需要继续找到叶子节点才可以获取数据
  • B 树的节点包括了 key-value，所以找到对应的 key 即可找到对应的 value，不用在继续寻找
  • 两种树各有优缺点和应用场景

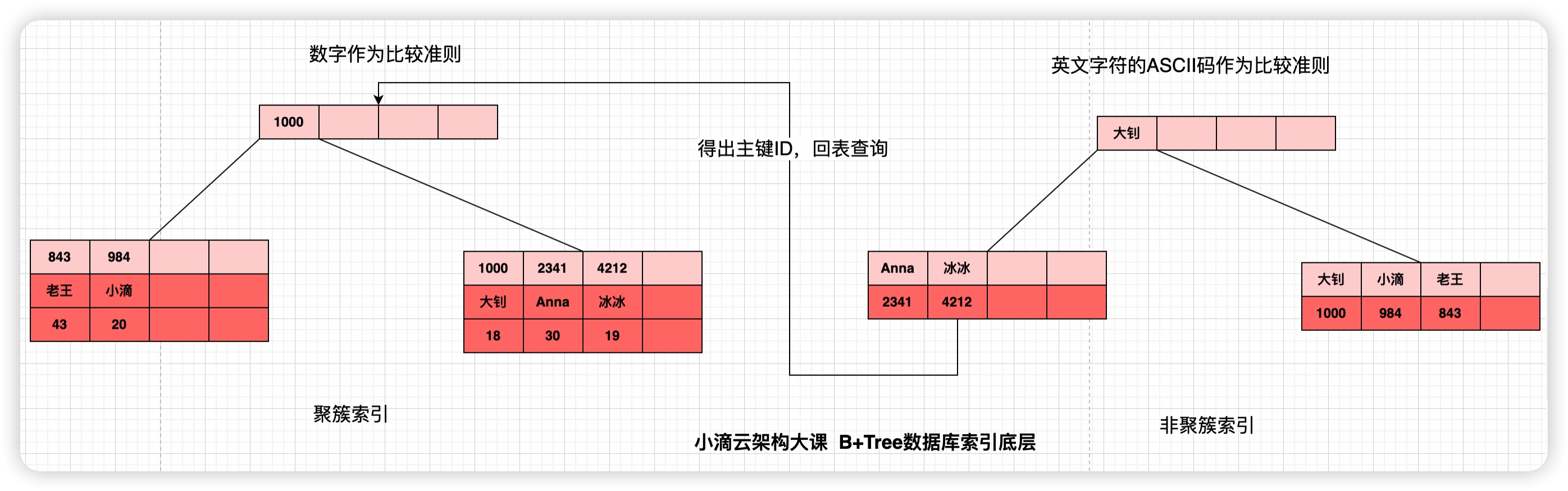
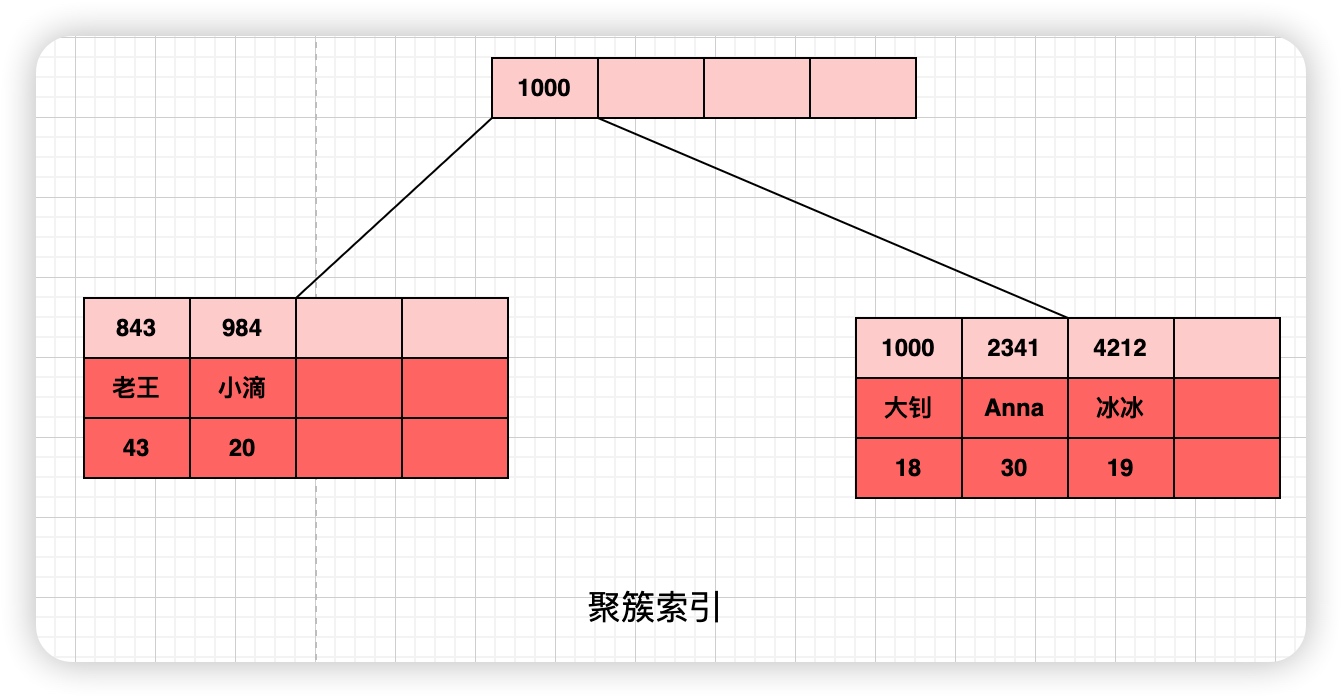
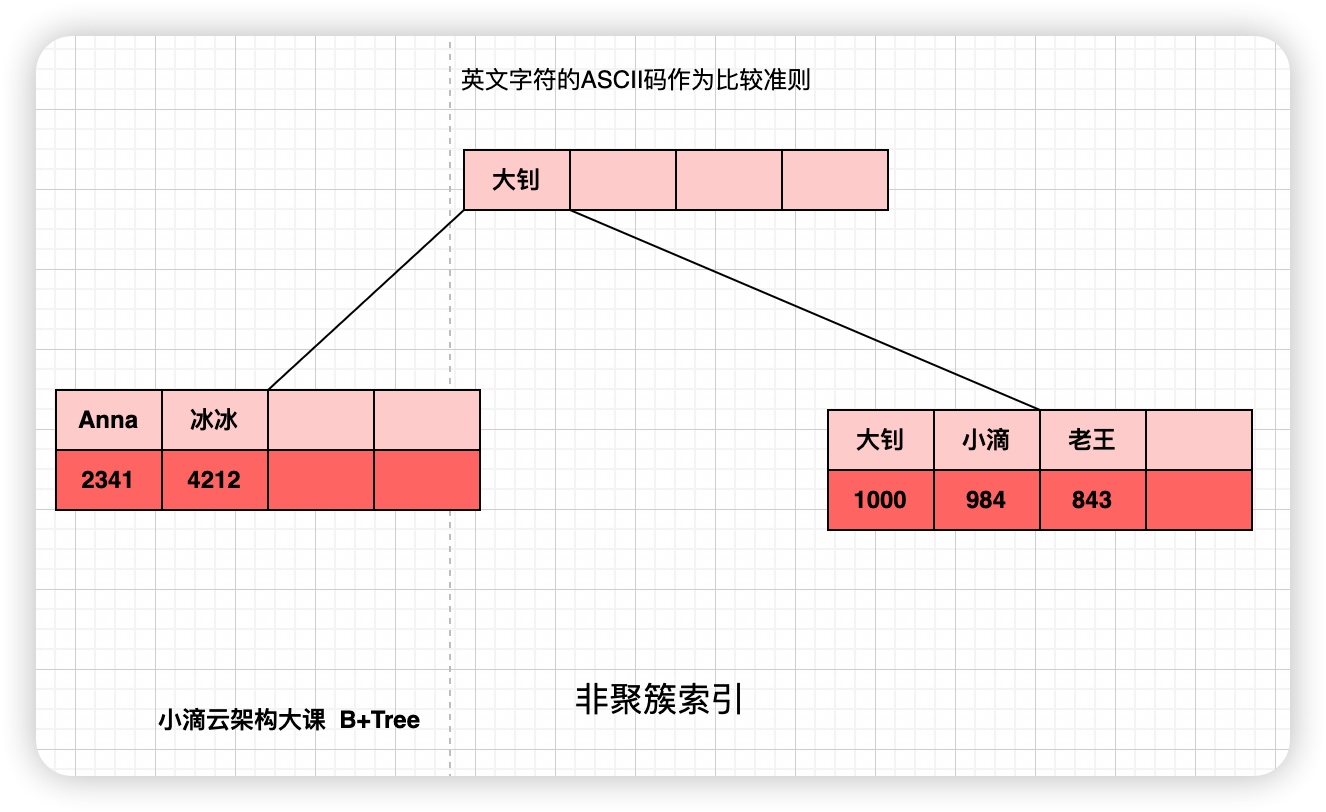
第 6 集 【重点】B+Tree 树应用之 Mysql 索引底层原理剖析

简介： B+Tree 树应用案例之 Mysql 索引底层原理剖析

• 背景

  • Mysql 数据库是大家用最多的，查询是最高频使用的操作
  • 在多数数据库的设计里面，会用 B-Tree 或 B+Tree 做索引提高查询效率

• 基于一张数据库的表数据进行查询（类似 mysql 的 user 表）

  • 构建索引：id 用做 key，然后 data 是数据的存储地址

  内存地址	id	phone	name	Age
  0xFS	843	13113777321	老王	43
  0xER	984	15738235423	小滴	20
  0x32	4212	121452354223	冰冰	18
  0x93	1000	124523563242	大钊	30
  0xAP	2341	135344432311	Anna	19
  0xSQ	.... 1 千万条数据

  • 精确查找 id=2341 的数据 select * from user where id = 2341

    • 未使用索引
      • 自上而下查找数据，一行行遍历，5 次才找到数据
    • 使用索引
      • id 建立主键索引（B+Tree 结构），对应的数据存储数据的地址，2 次找到数据，且数据量越多效果越明显
      • 根节点是常驻内存的，不需要进行 IO 操作

    

  • 范围查找 id>1000 和 id < 4212 的用户

    • 未使用索引
      • 自上而下查找数据，一行行遍历
    • 使用索引
      • id 建立主键索引（B+Tree 结构），由于本身是有序链表，所以顺序查找即可

• 大家是否会产生一个疑惑点

  • 如果把相关数据都放到 B+Tree 叶子节点上，拿查询的时候直接一次性就可以把数据获取了

  • 这个就是 Mysql 的 InnoDB 中的索引结构与 MyISAM 的索引结构最大区别了

    • InnoDB 引擎,表数据文件按 B+Tree 组织的，叶节点 data 域保存完整行数据, 树上的 key 就是主键, 以主键构建的 B+树索引

      • 这种索引叫做聚集索引（聚簇索引 clustered index）
      • 聚簇索引一般为主键索引，而主键一个表中只能有一个，所以聚集索引一个表只能有一个
      • 聚簇索引叶子节点存储的是行数据，而非聚簇索引叶子节点存储的是聚簇索引（通常是主键 ID）

      

    • MyISAM 引擎：索引文件和数据文件是分开的，索引结构的叶子节点放的是指向数据的主键（或者是地址）构建的 B+树索引

      • 这种索引叫做非聚集索引、二级索引、辅助索引（非聚簇索引 nonclustered index）
      • 非聚集索引一个表可以存在多个
      • 叶子节点中保存的不是实际数据，而是主键，获得主键值后去聚簇索引中获得数据行

      

• 注意

  • 非聚簇索引的叶子节点上存储的并不是真正的行数据，而是主键 ID 或记录的地址
  • 当使用非聚簇索引进行查询时，会得到一个主键 ID，再使用主键 ID 去聚簇索引上找真正的行数据，把这个过程称之为回表查询
  • 所以聚簇索引查询效率更高，而非聚簇索引需要进行回表查询，性能不如聚簇索引