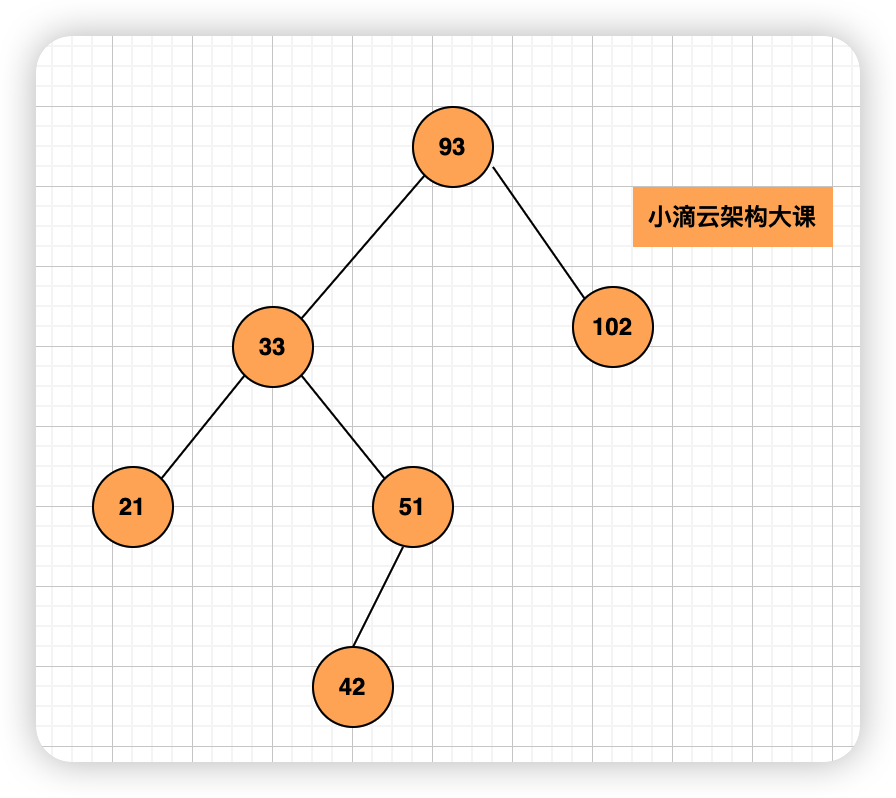
第28章 架构师必备的核心数据结构之二叉树

2025/04/11
posted in
数据结构和算法